Startseite → Forum → Matherätsel → Das angebundene Schaf
Forum
| Thema: Das angebundene Schaf |
|---|
| Jonas (Administrator, 334 Beiträge) am 11.11.2016 um 09:59 Uhr: |
| Konnten Sie die Länge der Leine bestimmen? Posten Sie Ihren Lösungsvorschlag hier. |
| majuraba (1 Beitrag) am 19.12.2016 um 09:34 Uhr: |
| Ich bin eine absolute Mathenull. Aber ist die Leine 1 km lang? |
| Ausblenden Anzeige: |
|
|
| Jonas (Administrator, 334 Beiträge) am 21.12.2016 um 21:47 Uhr: |
| Nein, bei 1 km käme das Schaf zwar bis zum Mittelpunkt der Weide, aber das ist weniger als die halbe Fläche der Weide. |
| Dorftrotel (2 Beiträge) am 23.12.2016 um 18:35 Uhr: |
| Habe eine Idee, aber keine ahung, wie ich das umformen soll... 0.5 * Pi * 1000² = Pi * r² - ( Pi * r² - 0,5 * Pi * 1000² ) wenn ich das dann umforme sieht das so aus: 0.5 * Pi * 1000² = Pi * r² - ( Pi * r² - 500000 * Pi ) schleißlich dann das Problem, wenn ich die Klammer auflöse: 0.5 * Pi * 1000² = Pi * r² - Pi * r² + 500000 * Pi 500000 * Pi = 500000 * Pi ist also richtig, was ich gerechnet habe, aber brauch ja das " r ", sonst bringt das richtig sein auch herzlich wenig |
| Jonas (Administrator, 334 Beiträge) am 23.12.2016 um 21:10 Uhr: |
| Die Gleichung sieht so aus, als hättest du zwei äquivalente Gleichungen ineinander eingesetzt. Z.B. ist x + y = 5 äquivalent zu x = 5 - y. Setzt man die zweite Gleichung in die erste ein, so erhält man: (5 - y) + y = 5 also: 5 = 5 |
| Dorftrotel (2 Beiträge) am 25.12.2016 um 12:16 Uhr: |
| Naja ich hab den überschneidenen Teil aus anderen herangehnsweisen aufgeschrieben und gleichgesetzt. 0.5 * Pi * 1000² ist der Teil in abhängigkeit des Feldes und Pi * r² - ( Pi * r² - 0,5 * Pi * 1000² ) ist der Teil in abhängigkeit des 2. kreises vom Seil also der ganze Kreis Pi*r² minus dem Teil der nicht im Feld drinn ist, also wieder der ganze Kreis Pi*r² minus dem Teil, der im Feld ist. Aber kann gut sein, dass das nichts bringt :D |
| Kloschkolov (55 Beiträge) am 26.12.2016 um 16:31 Uhr: |
| Hallo! Ich bin mir ziemlich sicher ich hab die Lösung! Die Länge der Leine des Schaafs muss ziemlich exakt 1,15872847301812 km sein. Der Lösungsweg ist allerdinds nicht ganz einfach und wird etwas dauern zum niederschreiben, ich reich ihn heute Abend nach wenn mein Sohn im Bett ist ;-) |
| Jonas (Administrator, 334 Beiträge) am 26.12.2016 um 17:06 Uhr: |
| Hallo! Die Lösung ist auf jeden Fall schon mal richtig. Freue mich schon auf den Lösungsweg und bin gespannt, ob es ein anderer als meiner ist. |
| Kloschkolov (55 Beiträge) am 26.12.2016 um 20:12 Uhr: |
| Ok dann wollen wir mal ^^ Ich hatte es zuerst mit reiner (Schul-)Geometrie versucht, da gelang es mir nicht wirklich die vielen Variablen zu bändigen. Danach hatte ich einen Ansatz über Funktionen und Integrale, welcher vermutlich auch funktioniert hätte wenn ich auf die schnelle ein Programm gefunden hätte welches mir Integralgleichungen nummerisch löst. Am Ende hab ich jetzt eine Vorüberlegung mit Hilfe von Funktionen und den Rest dann über relativ normale Geometrie gelöst. /Edit: Skizze 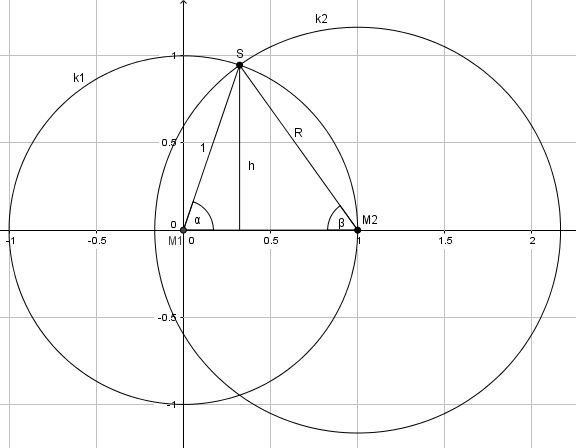 Zuerst habe ich das Problem in ein Koordinatensystem verlegt. M1 habe ich in den Ursprung gelegt, M2 auf die x-Achse in den Punkt (1|0). Danach habe ich erstmal nur die "obere Hälfte" des Problems betrachtet, also nur für positive y-Werte. Was letztendlich ja eine äquivalente Problemstellung ist, da die Figur ja Achsensymmetrisch zur x-Achse ist. Den gesuchten Radius vom 2. Kreis habe ich R genannt. Die beiden Halbkreise lassen sich über folgende Funktionen beschreiben: k1: y = (1-x^2)^0,5 k2: y = (R^2 - (x-1)^2)^0,5 Die Koordinaten des Schnittpunktes S, der beiden Kreise erhält man durch gleichsetzen und auflösen nach x. Also (1-x^2)^0,5 = (R^2 - (x-1)^2)^0,5 => x = 1 - 0,5R^2 Durch einsetzen in k1 erhält man die y-Koordinate von S: y = ( R^2 - 0,25 R^4 )^0,5 Jetzt habe ich M1, M2 und S zu einem Dreieck verbunden und die Höhe h durch S eingezeichnet (welche das große Dreieck in 2 kleine Teildreiecke teilt). => h = ( R^2 - 0,25 R^4 )^0,5 Im großen Dreieck habe ich den Winkel bei M1 a genannt und bei M2 b. Jetzt kann man für das linke Teildreieck sin a bilden und erhält: sin a = h / 1 = ( R^2 - 0,25 R^4 )^0,5 => a = arcsin (( R^2 - 0,25 R^4 )^0,5) Jetzt kann man für das rechte Teildreieck sin b bilden und erhält: sin b = h / R = ( R^2 - 0,25 R^4 )^0,5 / R = ( 1 - 0,25 R^2 )^0,5 => b = arcsin (( 1 - 0,25 R^2 )^0,5) Nun kann man sich endlich der eigentlichen Problemstellung widmen: Die Fläche welches das Schaaf abgrasen kann setzt sich zusammen aus den 2 Kreissektoren: A1 ist der Sektor um M1 mit Winkel a A2 ist der Sektor um M2 mit Winkel b Addiert man diese beiden Sektoren rechnet man ein Stück doppelt, nämlich das Dreieck M1M2S (A3). Die Fläche welche das Schaaf abgrasen kann soll genau die Hälfte des Halbkreises mit Radius 1 sein => A1 + A2 - A3 = 0,25Pi Die einzelnen Flächen lassen sich wie folgt berechnen A1 = a/2Pi * 1^2 * Pi = 0,5a = 0,5arcsin (( R^2 - 0,25 R^4 )^0,5) A2 = b/2Pi * R^2 * Pi = 0,5b R^2 = 0,5R^2 * arcsin (( 1 - 0,25 R^2 )^0,5) A3 = 0,5 * 1 * h = 0,5 ( R^2 - 0,25 R^4 )^0,5 Wenn man nun einsetzt hat man eine Gleichung welche nur von R abhängt. Diese muss man allerdings nummerisch lösen (lassen). Newton-Verfahren sollte z.B. klappen oder man lässt irgendein anderes Programm drauf los. Von Hand auflösen dürfte kaum möglich sein (falls doch lass ich mich da gerne belehren :-) ) Und so erhält man vorher schon erwähntes R = 1,15872847301812... |
| Jonas (Administrator, 334 Beiträge) am 26.12.2016 um 21:04 Uhr: |
| Sehr schön! Mein Lösungsweg (der jetzt übrigens online ist) ist anders, aber am Ende habe auch ich eine Gleichung numerisch lösen müssen und bin zur gleichen Lösung gekommen. Ich wüsste auch nicht, dass dieses Rätsel ohne ein numerisches Verfahren lösbar wäre. Aber auch ich lasse mich natürlich gern eines Besseren belehren. |
Die Community wurde geschlossen. Registrierungen und Logins sind nicht mehr möglich, die Beiträge stehen aber weiterhin zur Verfügung. Alle persönlichen Benutzerdaten wurden gelöscht.