Startseite → Forum → Matherätsel → Der 5-Euro-Schein
Forum
| Thema: Der 5-Euro-Schein |
|---|
| Jonas (Administrator, 334 Beiträge) am 28.10.2007 um 19:09 Uhr: |
| Wie lang ist der Knick im 5-Euro-Schein? Posten Sie die Lösung hier! |
| MrX (22 Beiträge) am 29.10.2007 um 12:04 Uhr: |
| Meiner Berechnung nach ist dieser Knick so ca genau 86,2786....mm lang |
| Ausblenden Anzeige: |
|
|
| Jonas (Administrator, 334 Beiträge) am 29.10.2007 um 16:51 Uhr: |
| Das stimmt nicht so ganz. Leider kann ich dir aber so nicht sagen, ob der Ansatz falsch war oder ob du dich nur vertippt hast. Poste doch einfach mal deinen Ansatz! |
| doro (2 Beiträge) am 10.12.2007 um 20:28 Uhr: |
| Mein Ansatz ergibt eine Länge von 73,78...mm. Durch das Falten ergeben sich ja zwei kongruente Trapeze. Was eigentlich nicht weiter wichtig ist, denn es kommt nur darauf an, dass man den Bereich rund um den Knick als zwei Dreiecke sehen kann. Deren Hypothenuse kann man berechen, was oben dokumentierte Zahl ergab. |
| Maxi (11 Beiträge) am 18.12.2007 um 21:14 Uhr: |
| Ich habe eine Länge von 69,786... mm. Die Falten stehen senkrecht auf den Diagonalen. Dadurch kann man mit der Hälfte der Diagonalen die Hälfte der Falte berechnen (Satz des Pythagoras). Das Ergebnis mal 2 und schon hat mans. |
| Manuel (68 Beiträge) am 21.12.2007 um 16:38 Uhr: |
| Ich habe noch einen anderen Lösungsweg gefunden. Er ist aber im Ansatz etwas komplexer, deshalb versuche ich es via skizze zu erklären: Zuerst zeichnet man ein Rechteck (Länge > Höhe; quer). Dann zeichnet man die Diagonale von oben links nach unten rechts ein. dann zeichnet man den Knick ein, der an der unteren Kante etwas links vom Mittelpunkt beginnt, die Diagonale im Mittelpunkt schneidet und an der oberen Kante rechts vom Mittelpunkt endet. Danach zeichnet man noch eine Senkrechte zur unteren Kante, die durch den Schnittpunkt Knick-obereKante führt. Die Punkte benenne ich so: Ecke unten links A, Ecke unten rechts B, Ecke oben rechts C, Ecke oben links D. Der Mittelpunkt ist M, der Punkt zwischen A und B links E, der daneben F und der Punkt zwischen C und D ist G. Jetzt hat man bei dem Winkel BDC den Winkel Alpha. bei M ist der Winkel im Dreieck DMG dann ein rechter Winkel (vom Falten her gegeben). Der letzte Winkel in diesem Dreieck, MGD, ist 90°-Alpha. Der Winkel gleich daneben, FGE, muss wieder Alpha sein, da er die Differenz vom rechten Winkel zu (90°-Alpha) bildet. Die Strecke GF entspricht der Breite. Jetzt rechnet man Alpha aus : tan Alpha = 62/120 . Dann rechnet man den Falt f aus: cos alpha = 62 / f. Also ist f = 62 / cos alpha = 62/ (cos(tan^-1(31/60))) = 69.786... Hoffe, es ist mehr oder weniger verständlich ... Falls man Grafiken raufladen kann, schreibt mir, damit ich eine Skizze hochladen kann. Gruss |
| Jonas (Administrator, 334 Beiträge) am 21.12.2007 um 17:01 Uhr: |
Zitat: Grafiken kann nur ich hochladen und im Forum einbinden. Wenn du willst, kannst du mir die Grafiken per E-Mail schicken. Ich lade sie dann hoch und füge sie in diesen Beitrag ein. edit: Hier die Zeichnung von Manuel: 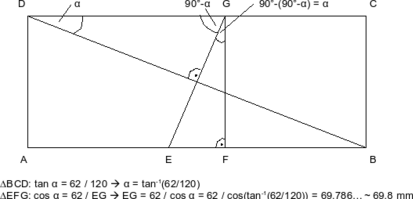 Achtung: In dieser Lösung ist ein kleiner Fehler: Hier wurde nur mit 120 mm statt mit 121 mm gerechnet. Mit 121 mm kommt EG = 69,66 mm heraus. |
| Manuel (68 Beiträge) am 22.12.2007 um 13:09 Uhr: |
| Ich hab sie jetzt mal digitalisiert, konnte aber deine E-Mail-Adresse nirgends finden - vllt habe ich auch zu wenig gesucht... Bei mir kommt nichts wenn ich auf das Kontaktformular gehe, und was ist mit dem Satz \"Alternativ können Sie mich auch unter erreichen.\" --> unter was? Lg Manuel |
| Jonas (Administrator, 334 Beiträge) am 22.12.2007 um 13:18 Uhr: |
| Die E-Mail-Adresse ist mit JavaScript geschützt. Du musst JavaScript einschalten, um sie sehen zu können. Die meisten Spambots können kein JavaScript. Deshalb schütze ich mich so gegen Spam. |
| Manuel (68 Beiträge) am 22.12.2007 um 16:29 Uhr: |
| Ach so. Firefox lässt ursprünglich ja alle JavaScripte zu, aber da es auch attacken geben kann via JavaScript, habe ich das FF-PlugIn \"NoScript\" installiert, welches standardmässig gar keine Scripts zulässt. Die Schattenseite ist aber, dass manche Funktionen nicht funktioniert (bis man es aktiviert). Ich habs jetzt geschickt. Gruss |
Die Community wurde geschlossen. Registrierungen und Logins sind nicht mehr möglich, die Beiträge stehen aber weiterhin zur Verfügung. Alle persönlichen Benutzerdaten wurden gelöscht.